De zeef begint bij 2. Elk getal is deelbaar door 1 en maakt die controle overbodig.
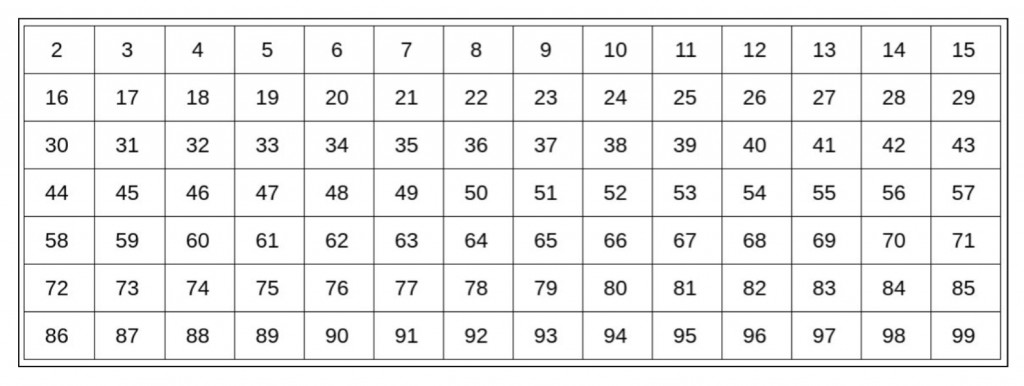
Figuur 1: de getallen 2 t/m 99 nu nog gebruikt als deler.
De zeef werkt als volgt: neem het eerste getal en streep alle veelvouden weg. De getallen 4 en 6 zijn veelvouden van 2. Een getal deelbaar door 6, is ook deelbaar door 2. De afbeelding hierboven is de startsituatie en de afbeelding hieronder toont het resultaat na toepassing van de zeef.

De overgebleven delers na het filteren met 7.
Ongeveer 26% van de delers blijft over door alleen de getallen 2, 3, 5 en 7 te gebruiken. Deze delers zijn allemaal priemgetallen. Bij de controle of een getal een priemgetal is, worden priemgetallen gebruikt.
Bovenstaande controle werkt snel, maar niet snel genoeg voor het controleren van grote getallen. Neem het getal 6.821.097.528.484.087, een getal met 16 cijfers. Met als laagste priemgetal 82.589.933, zijn 4.811.740 delers nodig om te bewijzen dat 6.821.097.528.484.087 geen priemgetal is. Het project Great Internet Mersenne Prime Search (GIMPS) heeft als doel steeds het grootst bewezen priemgetal te vinden. Er zijn een oneindig aantal getallen, hierdoor ook een oneindig aantal priemgetallen. Sinds 1996 heeft GIMPS steeds het grootst bewezen priemgetal gevonden. De formule die GIMPS gebruikt is 2^p -1, waarbij p een priemgetal is (let op: het toepassen van deze formule levert niet altijd een priemgetal op). Op het moment van schrijven is het grootst bewezen priemgetal 2^82589933-1, een getal met 24.862.048 cijfers.












